Resection, or Finding the  Coordinates

of a New Control Point

The term “Resection” is used to describe the practice of identifying the coordinate location of a new control point or monument from two established points. Frequently surveyors discover that the work that they need to accomplish is not visible from the control points previously set and thus they need to establish a new point on which to set up their instrument. The resection method of establishing coordinates is one method that can be used to place coordinates on a new point. 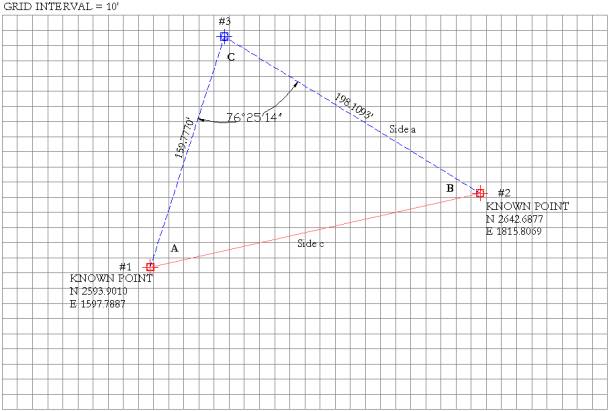This method assumes that you can see two existing control points (#1 & #2) from the proposed new point #3.  The diagram below provides the “known” information referred to in step #2. All additional information needed will be calculated in the steps below.

Step 1

Set instrument on new control point # 3 and back sight control point #1.

Set your backsight azimuth on the instrument to read 0.00'00".

Measure the distance from #3 to #1.

Rotate instrument to control point #2.

Record horizontal azimuth.

Measure the distance from #3 to #2.

Step 2

After collecting data in the field, what do you know? You have the distance from your new control point to each of the established points, and you have measured the internal angle (C) between the two lines of sight.

You also know the coordinates of control point #1 and #2, although BG-Map and AutoCAD work with the order reversed from your surveying instrument. To calculate the location of point #3, reverse the coordinates to read Y - X as shown on this diagram.

Step 3

Next, you need to calculate the length of the line between your two known points (between #1 and #2). To do this use the following equation:

Thus: (2593.9010 - 2642.6877)  +  (1597.7887 - 1815.8069)  = 49,912.0776.  The square root of 49,912.0776 is 223.4101. Line #1 - #2 is 223.4101 feet in length.

Step 4

Calculate the Azimuth of the line #1 - #2 using the following formula:

This results in the following:

or 4.4126, which is the inverse tangent, or Arc tangent of the azimuth of the line. By using the Arc tangent or inverse tangent facility on a calculator, the result will be an azimuth of 77.23' 11". For calculating purposes, calculate the decimal equivalent, which is 77.3864.

Step 5

The next exercise is to calculate the value of internal angle "A". The formula for this is:

= -1.7002 which is the tangent of internal angle "A". Use the inverse tangent or Arc tangent function to arrive at -59.5378. This is a decimal equivalent of -59d 32'16”, which is the value that would be measured in the field for internal angle "A".

NOTE: The value for internal angle "C" as recorded in the field was 76d 25' 14". This must be converted to its decimal equivalent before generating sine or cosine values for factoring.

Step 6

Figure the azimuth of line #1 - #3 by adding the decimal value of internal angle "A" to the calculated decimal azimuth for line #1 - #2. Thus, -59.5378 + 77.3864 = 17.8486, which is the decimal azimuth for line #1 - #3 as viewed from the position of "known point #1". Add this value to the decimal azimuth for internal angle "C". Subtract the combined value from 180.0000 to discover the value of internal angle "B" which should be 85.7309 decimal degrees.

Step 7

The last step is to calculate the Latitude and Departure of the new point from the location of a known point using the information generated thus far. We will calculate the latitude and departure of point #3 beginning from point #1.

The formula for calculating the Latitude, or distance away in the north/south direction is;

Latitude = Distance x cosine of the decimal azimuth.

Thus, this factor for point #3 is 159.7770 x 0.9519 = 152.0869

The formula for calculating the Departure, or distance in the east/west direction is; Departure = Distance x sin of the decimal azimuth. Thus, this factor for point #3 is 159.7770 x .3065 = 48.9721.

Finally, Add the Latitude value to the North coordinate of point #1 and the Departure value to the East coordinate and the resulting values are the coordinates for newly established Point #3.

2593.9010 + 152.0869 = N 2745.9879

1597.7887 +   48.9721 = E 1646.7608

The final redundant check is to calculate the reverse azimuth for line #1 - #2 by adding 180 to the decimal equivalent of 77d 23' 11". The resulting value of 257.3864 is the decimal equivalent of the reverse azimuth. Add to this the calculated value for internal angle "B" to derive the decimal azimuth of line #2 - #3 and again, calculate the latitude and departure values and add them to the appropriate Northing and Eastings for point #2. They should result in coordinates for point #3 that are very close to those obtained in the previous work. There will be some variation due to rounding within the formulae. That can be factored out by balancing, but that is for another day......