Notes and Suggestions
for Botanical Garden Surveyors - Part 14
By
Wayne Cahilly,
The New York Botanical
Garden
© 2003 The New York Botanical Garden
Wayne Cahilly is Manager
of the Institutional Mapping Department at The New York Botanical Garden.
Please feel free to contact him with any questions at
wcahilly@nybg.org
|
|
Using an Inverse Traverse Calculation to Locate a Lost Control
Point |
|
|
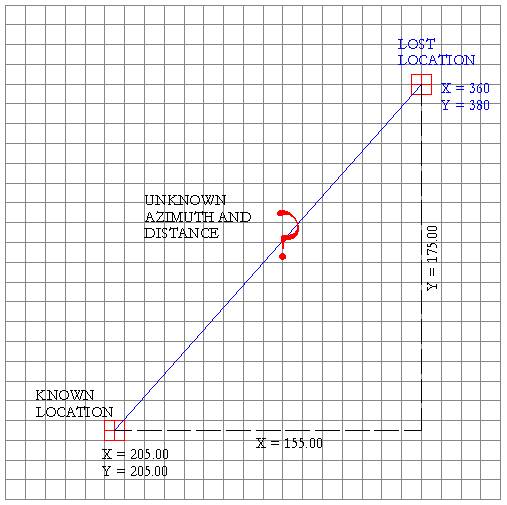
Here’s
a technique for finding a lost control point if you know its coordinates and
can locate another nearby control point.
Determining polar coordinates from known
rectangular coordinates is a fairly straightforward process. This process
requires three steps, deriving the rectangular difference between the two
points, determining the polar distance, and determining the azimuth. To derive the rectangular difference between two
points, subtract the Northing (Y) of the known location from the Northing (Y)
of the lost location. In this example that returns a product of +175.00. Secondly, subtract the Easting (X) of the known
location from the Easting (X) of the lost location returning a product of
+155.00. Thus, the rectangular difference between the known
location and the lost location is a difference of North 175 and East 155
feet. These distances form two know sides of a right triangle and are shown
in dashed lines on the diagram. Step Two: Determine the distance from the known
point to the lost point. To accomplish this the following equation is used:
The result is 233.7734 or the polar distance from
the known to the lost point. Step 3: Determining the azimuth of the line from
the known to the lost point. The equation used is:
ArcTan (Y/X) This results in the following solution: (Y/X) or
175.00/155.00 = 1.1290 The ArcTangent, or inverse tangent of 1.1290 is
48.4682, the decimal azimuth for the line from the known to the lost
location. Convert to degrees, minutes, and seconds with a calculator, set up
your total station on the known location, level and backsight, then rotate
the scope to an azimuth of 48*28'06" and measure a distance of 233.7734
to the lost point. In calculating the difference in Northing and
Easting (Y and X) be sure to keep track of positive and negative numbers. If
the Northing of the lost location is a smaller number than the Northing of
your known location then your lost point will have a negative Northing. If
the lost point has a Easting that is smaller than your known location, then
the lost point is said to have a negative Easting. For example, if the lost point had coordinates of
Northing = 30, Easting = 50 the results of calculating the rectangular
difference would be X -155.00 Y -175.00.
which is
the same distance as we saw previously. The azimuth results of the above variation on the data would be ArcTangent -175.00/-155.00 or a decimal
azimuth of 48.4682 but because our Rectangular difference in the North/South(Y
= -175.00) direction was negative, this azimuth is added to 180 resulting in
an actual decimal azimuth of 228.4682 which can be converted to 228*28'06. When the Northing (Y) is a positive number, the
azimuth will be north of the east-west line, or between 270 degrees and 90
degrees. If the resulting easting is positive as well, the azimuth will be in
the northeast quadrant between 0 and 90 degrees and the calculation returns
the actual azimuth. However, if the easting is negative, the azimuth will be
in the northwest quadrant and the result of the calculation must be
subtracted from 360 degrees. When the results of the rectangular difference
calculations return a negative northing then the resulting azimuth will be
below the east-west line, or between 90 degrees and 270 degrees. The azimuth
is added to 180 degrees. A product of the azimuth calculation that is
positive (45 degrees for example) will be added to 180 resulting in 225
degrees or an azimuth in the southwest quadrant. If the result had been
negative (-45 degrees for example) then when this was added to 180 the result
would be 135 degrees, or an azimuth in the southeast quadrant. |
|
|
|